本文共 6078 字,大约阅读时间需要 20 分钟。
Core Text是和Core Graphics配合使用的,一般是在UIView的drawRect方法中的Graphics Context上进行绘制的。 且Core Text真正负责绘制的是文本部分,图片还是需要自己去手动绘制,所以你必须关注很多绘制的细节部分。
一、CoreText框架
CoreText 框架中最常用的几个类:
(1)、 (2)、 (3)、 (4)、 (5)、 (6)、 (7)、 (8)、 (9)、 (10)、 (11)、二、Core Text知识准备
1、字体(Font)
和我们平时说的字体不同,计算机意义上的字体表示的是同一大小,同一样式(Style)字形的集合。从这个意义上来说,当我们为文字设置粗体,斜体时其实是使用了另外一种字体(下划线不算)。而平时我们所说的字体只是具有相同设计属性的字体集合,即Font Family或typeface。

(1)、字体(Font)
是一系列字号、样式和磅值相同的字符(例如:10磅黑体Palatino)。现多被视为字样的同义词 (2)、字面(Face) 是所有字号的磅值和格式的综合 (3)、字体集(Font family) 是一组相关字体(例如:Franklin family包括Franklin Gothic、Fran-klinHeavy和Franklin Compressed) (4)、磅值(Weight) 用于描述字体粗度。典型的磅值,从最粗到最细,有极细、细、book、中等、半粗、粗、较粗、极粗 (5)、样式(Style) 字形有三种形式: Roman type是直体; oblique type是斜体; utakuc type是斜体兼曲线(比Roman type更像书法体)。 (6)、x高度(X height) 指小写字母的平均高度(以x为基准)。磅值相同的两字母,x高度越大的字母看起来比x高度小的字母要大 (7)、Cap高度(Cap height) 与x高度相似。指大写字母的平均高度(以C为基准) (8)、下行字母(Descender) 例如在字母q中,基线以下的字母部分叫下伸部分 (9)、上行字母(Ascender) x高度以上的部分(比如字母b)叫做上伸部分 (10)、基线(Baseline) 通常在x、v、b、m下的那条线 (11)、描边(Stroke) 组成字符的线或曲线。可以加粗或改变字符形状 (12)、衬线(Serif) 用来使字符更可视的一条水平线。如字母左上角和下部的水平线。 (13)、无衬线(Sans Serif) 可以让排字员不使用衬线装饰。 (14)、方形字(Block) 这种字体的笔画使字符看起来比无衬线字更显眼,但还不到常见的衬线字的程度。例如Lubalin Graph就是方形字,这种字看起来好像是木头块刻的一样 (15)、手写体脚本(Calligraphic script) 是一种仿效手写体的字体。例如Murray Hill或者Fraktur字体 (16)、艺术字(Decorative) 像绘画般的字体 (17)、Pi符号(Pisymbol) 非标准的字母数字字符的特殊符号。例如Wingdings和Mathematical Pi (18)、连写(Ligature) 是一系列连写字母如fi、fl、ffi或ffl。由于字些字母形状的原因经常被连写,故排字员已习惯将它们连写。2、字符(Character)和字形(Glyphs)
排版过程中一个重要的步骤就是从字符到字形的转换,字符表示信息本身,而字形是它的图形表现形式。字符一般就是指某种编码,如Unicode编码,而字形则是这些编码对应的图片。但是他们之间不是一一对应关系,同个字符的不同字体族,不同字体大小,不同字体样式都对应了不同的字形。而由于连写(Ligatures)的存在,多个字符也会存在对应一个字形的情况。
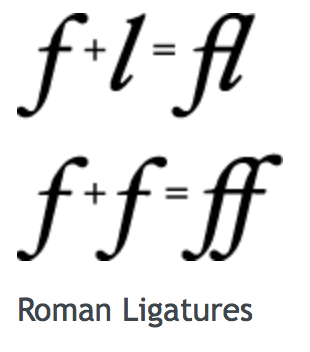 下面就来详情看看字形的各个参数也就是所谓的字形度量Glyph Metrics
下面就来详情看看字形的各个参数也就是所谓的字形度量Glyph Metrics 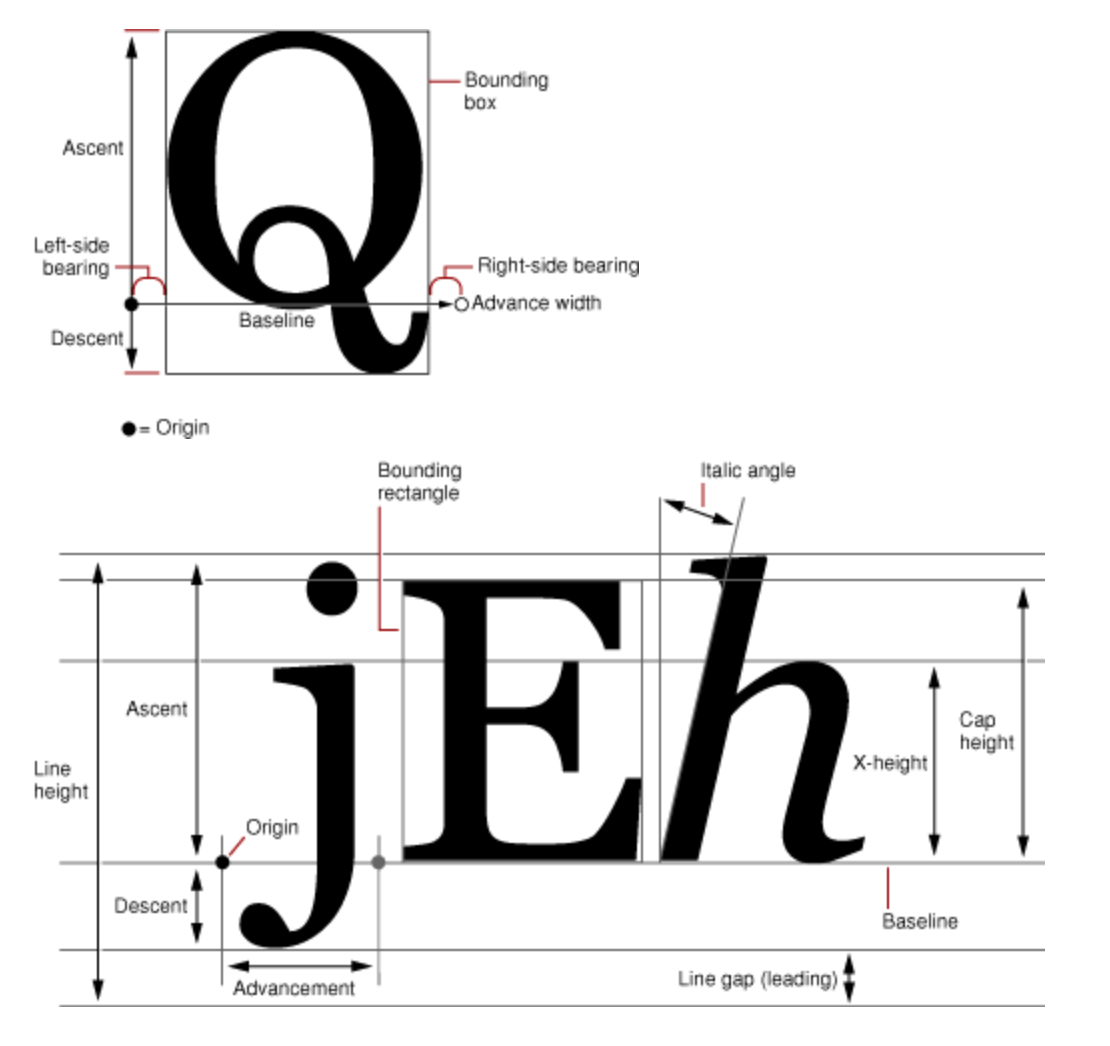 (1)、边界框 bbox(bounding box) 这是一个假想的框子,它尽可能紧密的装入字形。 (2)、基线(baseline) 一条假想的线,一行上的字形都以此线作为上下位置的参考,在这条线的左侧存在一个点叫做基线的原点, (3)、上行高度(ascent) 从原点到字体中最高(这里的高深都是以基线为参照线的)的字形的顶部的距离,ascent是一个正值 (4)、下行高度(descent) 从原点到字体中最深的字形底部的距离,descent是一个负值(比如一个字体原点到最深的字形的底部的距离为2,那么descent就为-2) (5)、行距(line gap) line gap也可以称作leading(其实准确点讲应该叫做External leading),行高line Height则可以通过 ascent + |descent| + linegap 来计算。 (6)、字间距(Kerning) 字与字之间的距离,为了排版的美观,并不是所有的字形之间的距离都是一致的,但是这个基本步影响到我们的文字排版。 (7)、基础原点(Origin) 基线上最左侧的点。
(1)、边界框 bbox(bounding box) 这是一个假想的框子,它尽可能紧密的装入字形。 (2)、基线(baseline) 一条假想的线,一行上的字形都以此线作为上下位置的参考,在这条线的左侧存在一个点叫做基线的原点, (3)、上行高度(ascent) 从原点到字体中最高(这里的高深都是以基线为参照线的)的字形的顶部的距离,ascent是一个正值 (4)、下行高度(descent) 从原点到字体中最深的字形底部的距离,descent是一个负值(比如一个字体原点到最深的字形的底部的距离为2,那么descent就为-2) (5)、行距(line gap) line gap也可以称作leading(其实准确点讲应该叫做External leading),行高line Height则可以通过 ascent + |descent| + linegap 来计算。 (6)、字间距(Kerning) 字与字之间的距离,为了排版的美观,并不是所有的字形之间的距离都是一致的,但是这个基本步影响到我们的文字排版。 (7)、基础原点(Origin) 基线上最左侧的点。 
3、坐标系
传统的Mac中的坐标系的原点在左下角,比如NSView默认的坐标系,原点就在左下角。但Mac中有些View为了其实现的便捷将原点变换到左上角,像NSTableView的坐标系坐标原点就在左上角。
iOS UIKit中,UIView是以左上角为原点,而Core Text一开始的定位是使用与桌面应用的排版系统,桌面应用的坐标系是以左下角为原点,即Core Text在绘制的时候也是参照左下角为原点进行绘制的,所以需要对当前的坐标系进行处理。
实际上,Core Graphic 中的context也是以左下角为原点的, 但是为什么我们用Core Graphic 绘制一些简单的图形的时候不需要对坐标系进行处理呢,是因为通过这个方法UIGraphicsGetCurrentContext()来获得的当前context是已经被处理过的了,用下面方法可以查看指定的上下文的当前图形状态变换矩阵。
- 方法一
//因为Core Text要配合Core Graphic 配合使用的,如Core Graphic一样,绘图的时候需要获得当前的上下文进行绘制CGContextRef context = UIGraphicsGetCurrentContext();NSLog(@"当前context的变换矩阵 %@", NSStringFromCGAffineTransform(CGContextGetCTM(context)));//翻转当前的坐标系(因为对于底层绘制引擎来说,屏幕左下角为(0,0))CGContextSetTextMatrix(context, CGAffineTransformIdentity);//设置字形变换矩阵为CGAffineTransformIdentity,也就是说每一个字形都不做图形变换CGAffineTransform flipVertical = CGAffineTransformMake(1,0,0,-1,0,self.bounds.size.height);CGContextConcatCTM(context, flipVertical);//将当前context的坐标系进行flipNSLog(@"翻转后context的变换矩阵 %@", NSStringFromCGAffineTransform(CGContextGetCTM(context)));
打印结果为:
当前context的变换矩阵 [2, 0, 0, -2, 0, 800]翻转后context的变换矩阵 [2, 0, 0, 2, 0, 0]
- 方法二
//因为Core Text要配合Core Graphic 配合使用的,如Core Graphic一样,绘图的时候需要获得当前的上下文进行绘制CGContextRef context = UIGraphicsGetCurrentContext();NSLog(@"当前context的变换矩阵 %@", NSStringFromCGAffineTransform(CGContextGetCTM(context)));//翻转当前的坐标系(因为对于底层绘制引擎来说,屏幕左下角为(0,0))CGContextSetTextMatrix(context, CGAffineTransformIdentity);CGContextTranslateCTM(context, 0, self.bounds.size.height);CGContextScaleCTM(context, 1.0, -1.0);NSLog(@"翻转后context的变换矩阵 %@", NSStringFromCGAffineTransform(CGContextGetCTM(context)));
打印:
当前context的变换矩阵 [2, 0, 0, -2, 0, 800]翻转后context的变换矩阵 [2, 0, -0, 2, 0, 0]
可以发现变换矩阵与CGAffineTransformIdentity的值[1, 0, 0, 1, 0, 0]是不相同的,并且与设备是否为Retina屏和设备尺寸相关。他的作用是将上下文空间坐标系进行翻转,并使原来的左下角原点变成左上角是原点,并将向上为正y轴变为向下为正y轴。 所以在使用drawRect的时候,当前的context已经被做了一次翻转,如果不对当前的坐标系进行处理,会发现,绘制出来的文字是镜像上下颠倒的。所以在UIView的drawRect方法中的context上进行Core Text绘制之前需要对context进行一次Flip。
三、Core Text对象模型
1、绘制流程
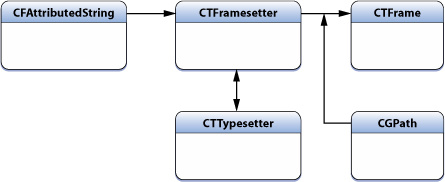
(1)、CFAttributedStringRef
属性字符串,用于存储需要绘制的文字字符和字符属性
(2)、CTFramesetterRef
framesetter对应的类型是 CTFramesetter,通过CFAttributedStringRef进行初始化,它作为CTFrame对象的生产工厂,负责根据path生产对应的CTFrame;
(3)、CTFrame
CTFrame是可以通过CTFrameDraw函数直接绘制到context上的,当然你可以在绘制之前,操作CTFrame中的CTLine,进行一些参数的微调;
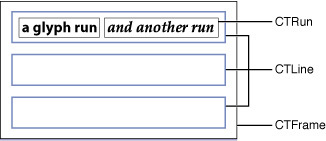
(3)、CTLine
在CTFrame内部是由多个CTLine来组成的,每个CTLine代表一行;可以看做Core Text绘制中的一行的对象 通过它可以获得当前行的line ascent,line descent ,line leading,还可以获得Line下的所有Glyph Runs;
(4)、CTRun
或者叫做 Glyph Run,每个CTLine又是由多个CTRun组成的,每个CTRun代表一组显示风格一致的文本,是一组共享想相同attributes(属性)的字形的集合体;
总结:
CTFramesetter是由CFAttributedString(NSAttributedString)初始化而来,可以认为它是CTFrame的一个Factory,通过传入CGPath生成相应的CTFrame并使用它进行渲染:直接以CTFrame为参数使用CTFrameDraw绘制或者从CTFrame中获取CTLine进行微调后使用CTLineDraw进行绘制。CTFrame 作为一个整体的画布(Canvas),其中由行(CTLine)组成,而每行可以分为一个或多个小方块(CTRun)。注意:你不需要自己创建CTRun,Core Text将根据NSAttributedString的属性来自动创建CTRun。每个CTRun对象对应不同的属性,正因此,你可以自由的控制字体、颜色、字间距等等信息。
2、通常处理步聚
- 获取上下文
- 翻转坐标系
- 创建NSAttributedString
- 根据NSAttributedString创建CTFramesetterRef
- 创建绘制区域CGPathRef(该CGPathRef是库CoreGraphics里边的,初始原点为左上角;翻转后,原点为左下角)
- 根据CTFramesetterRef和CGPathRef创建CTFrame
- CTFrameDraw绘制。
3、点击判断
绘制只是显示,点击事件就需要一个判断了。
CTFrame 包含了多个CTLine,并且可以得到各个line的其实位置与大小。判断点击处在不在某个line上。CTLine 又可以判断这个点(相对于ctline的坐标)处的文字范围。然后遍历这个string的所有NSTextCheckingResult,根据result的rang判断点击处在不在这个rang上,从而得到点击的链接与位置。
4、图文混排
上面说了这么多对也没一个东西和图片绘制有关系,其实吧,Core Text本身并不支持图片绘制,图片的绘制你还得通过Core Graphics来进行。只是Core Text可以通过CTRun的设置为你的图片在文本绘制的过程中留出适当的空间。这个设置就使用到CTRunDelegate了,看这个名字大概就可以知道什么意思了,CTRunDelegate作为CTRun相关属性或操作扩展的一个入口,使得我们可以对CTRun做一些自定义的行为。为图片留位置的方法就是加入一个空白的CTRun,自定义其ascent,descent,width等参数,使得绘制文本的时候留下空白位置给相应的图片。然后图片在相应的空白位置上使用Core Graphics接口进行绘制。
使用CTRunDelegateCreate可以创建一个CTRunDelegate,它接收两个参数,一个是callbacks结构体,一个是所有callback调用的时候需要传入的对象。 callbacks的结构体为CTRunDelegateCallbacks,主要是包含一些回调函数,比如有返回当前run的ascent,descent,width这些值的回调函数,至于函数中如何鉴别当前是哪个run,可以在CTRunDelegateCreate的第二个参数来达到目的,因为CTRunDelegateCreate的第二个参数会作为每一个回调调用时的入参。